pasobafter.blogg.se - Frequency distribution table on excel

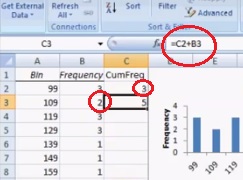
The next column is the Percentage column.Thus, the cumulative frequency is 3, meaning we have 3 participants in the 34 to 54 age group. However, in the second row, the frequency for the 35–44 interval ( i.e., 1) is added to the frequency for the 45–54 interval ( i.e. Since this is the first row, the cumulative frequency is the same as the frequency. Here we add the cumulative frequency of the previous row to the frequency of the current row. The fourth column is the Cumulative frequency column.Record the number of times a result appears between the lower and upper values. The third column is the Frequency column.For example, you would put the number 44 in the first row. Place the upper value of the result intervals.

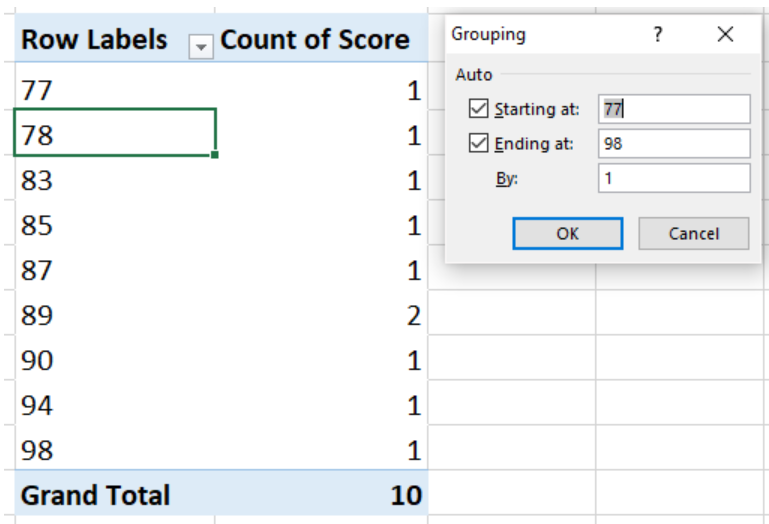
The next column is the Upper value column.For example, in the first row, you would put the number 35. In the first column or the Lower value column, list the lower value of the result intervals.Create a table similar to the frequency distribution table but with three extra columns.Since 36 is the lowest age and 92 is the highest age, start the intervals at 35 to 44 and end the intervals with 85 to 94. In this case, intervals of 10 are appropriate. Divide the results into intervals, and then count the number of results in each interval.Use the following steps to present these data in a cumulative frequency distribution table. The ages of the participants were recorded as follows: It looks almost the same as a frequency distribution table but it has added columns that give the cumulative frequency and the cumulative percentage of the results, as well.Īt a recent chess tournament, all 10 of the participants had to fill out a form that gave their names, address and age. Your frequency distribution table for this exercise should look like this:Ī cumulative frequency distribution table is a more detailed table.

Add up the number of tally marks in each row and record them in the final column entitled Frequency.

When you reach your fifth tally mark, draw a tally line through the preceding four marks to make your final frequency calculations easier to read. The next result is a 2, so place a tally mark in the row beside the 2, and so on. For example, the first result is a 1, so place a tally mark in the row beside where 1 appears in the interval column ( Number of cars).

Read the list of data from left to right and place a tally mark in the appropriate row.

Label these columns Number of cars, Tally and Frequency.

Make a table with separate columns for the interval numbers (the number of cars per household), the tallied results, and the frequency of results in each interval.

In this case, the intervals would be the number of households with no car (0), one car (1), two cars (2) and so forth.

Divide the results ( x) into intervals, and then count the number of results in each interval.

Use the following steps to present this data in a frequency distribution table. In each of 20 homes, people were asked how many cars were registered to their households.